Guessing

Sometimes you need to guess in Minesweeper. The optimal guessing strategy depends on whether your goal is to win or to win fewer games more quickly. New players often make the mistake of guessing instead of learning how to solve patterns.

The first strategy is to guess quickly. This is the best approach when there is no possibility of obtaining further information. It can also be effective if you are happy losing often in order to win fewer games but with better scores.

The second strategy is to guess only when you are forced to guess. If the squares touch other unopened squares, solve the rest of the board first in the hope that approaching from a different direction will eliminate the guess. However, many professionals guess immediately to avoid incurring the time it takes to move the mouse to an easier location.

A third strategy is to practice playing with no flags so you become better at looking for empty squares. Players who enjoy flagging often make the mistake of guessing a mine location and chording when they could have opened a safe square instead.

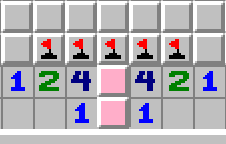This 50:50 guess is unavoidable. The best strategy is to guess quickly.

The pink squares are a 50:50 guess. The first strategy guesses quickly. The second strategy solves the rest of the board and hopes new information eliminates the guess.

There could be 1, 2 or 3 mines in these four squares. The second strategy solves the rest of the board to determine the number of mines. If there are 1 or 3 mines no guessing is needed.

You cannot deduce the mines. The third strategy forgets about mines and opens the safe pink squares. If each pink square is a 1 the blue squares can also be opened.

A fourth strategy makes the most useful guess. Sometimes one option eliminates another guess or makes the rest of the board easier to solve. For example, when there is a 33:66 situation on a row it is best to open the right or left squares. Opening the middle square will force you to make a second guess.

A fifth strategy considers probability. The mine density on Beginner (8x8) and Intermediate (16x16) is 0.156 and on Expert (16x30) is 0.206. When there is a 50:50 guess it is actually safer to open a random square! Edges are more likely to be openings than squares near the middle. A special case is the top left corner where the probability of being a mine doubles after the first click (due to mine shifting).

Avoid unnecessary guesses. Instead of opening three squares in a row open the yellow squares first so you have time to react if the middle square is a mine.

If you open the middle square you need to make another guess. The fourth strategy opens the blue square to eliminate the guess.

There are multiple 50:50 guesses. The fourth strategy opens a useful square. If the blue square is a 3 or 7 it eliminates guessing. If the green square is 3 or 6 it could also eliminate guessing.

There are multiple 50:50 guesses. The fifth strategy opens a 'random' square. On Expert the blue square is 20:80, does not touch a 50:50 and is on an edge so might be an opening.

The sixth strategy is to calculate probability. This is the best strategy for winning games but can be complicated and time consuming. Local probability is easy to calculate but global probability is much more difficult. For example, it is easy to calculate that one mine in two squares is 50:50 but what if probability depends on all possible mine arrangements for the rest of the board? Sean Barrett has written an excellent guide to Minesweeper Advanced Tactics.

The following example considers all six strategies. The first strategy is to guess quickly and hope for the best. This approach will give the best score if you survive. The second strategy is solving the rest of the board to determine the number of mines remaining. There are 79 possible mine arrangements but only 1 solution has 9 mines. The third strategy opens a safe square but in this case there are none. The fourth strategy makes a useful guess. In this case there is one square (I) that solves the board if it is a 4 or 7. The fifth strategy guesses a square that does not touch a number (B, C, F, G) hoping Expert density of 0.206 comes to the rescue. The sixth strategy calculates global mine probability which ranges from 0.392 (D, K) to 0.798 (J).

Three local 50:50 guesses.

Three local 66:33 guesses.

Preparing to calculate.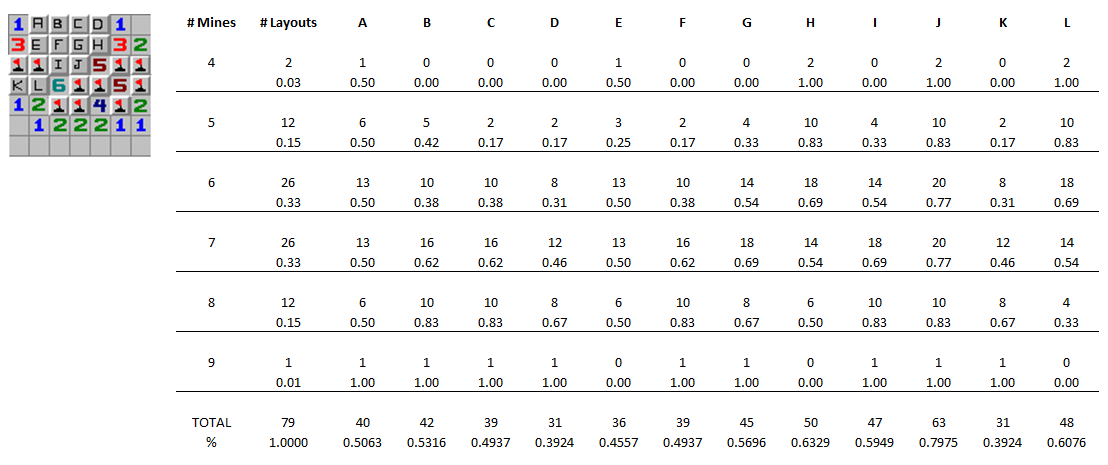

Global probabilities.